几天没写博客了,这几天在看一些课外书,不过今天看了一篇论文,Instance Segmentation by Jointly Optimizing Spatial Embeddings and Clustering Bandwidth,它是之前EmbedMask那篇论文中的可学习间隙的来源,这篇论文说主要提出了一种新的损失,而我觉得论文的主要贡献是提出了可学习的间隙margin以及在提高实时性的同时,保持了高的准确度。
网络结构
我们直接来看网络结构图。
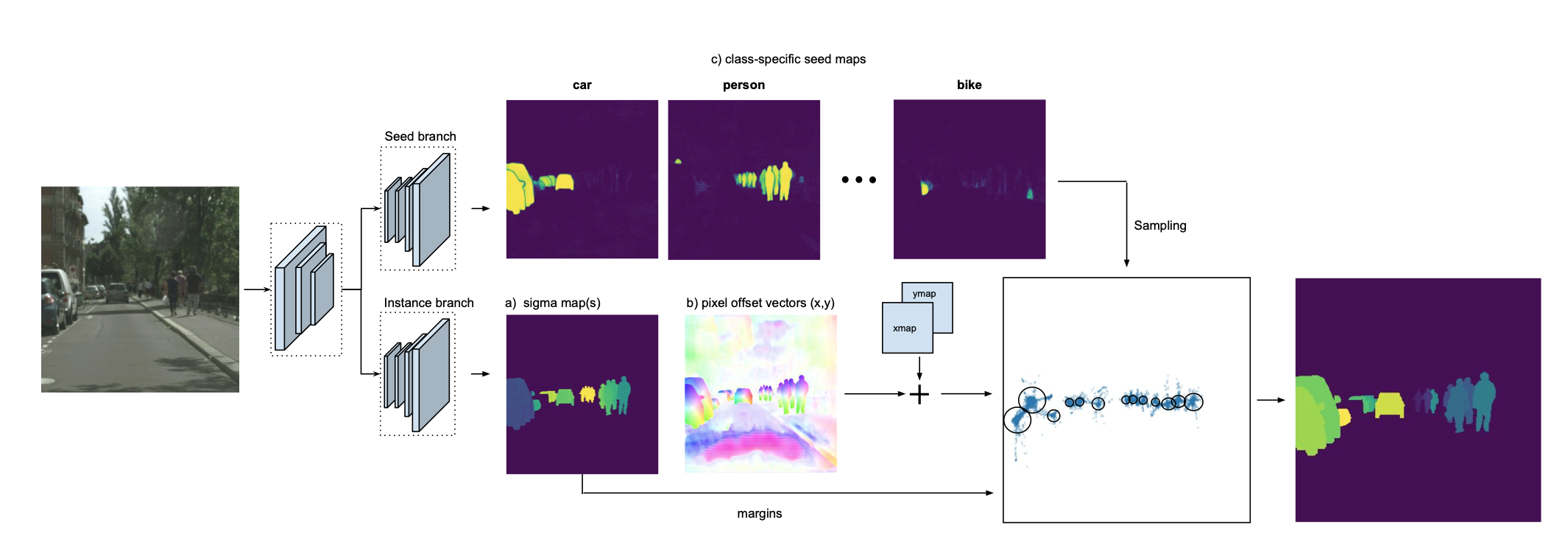
网络主要分为两个分支,上面的分支用来预测每个语义类别的种子图seed map,这个种子图呢,是一个分数图,靠近实例对象的中心点对应会有一个高的分数,而离中心点比较远的分数则比较低,下面的分支呢,输出offset map和间隙$\sigma$,offset map与坐标向量(xmap,ymap)相加构造成像素点的embedding。随后由seed map确定实例对象的中心点位置,取对应位置的$\sigma$作为间隙,通过计算embedding的距离(或者说是相似度)来确定实例分割的结果。
网络细节
seed map
查看源码发现呢,这个种子图,并不是像网络结构图中那样分了成了多张,而只是一张包含了所有语义对象的图并且用损失函数(如下)在语义对象上进行约束。
\[L_{seed} = \frac{1}{N}\sum_{i}^{N}\mathbf{1}_{\{s_i \in S_k\}}||s_i-\phi_k(e_i)||^2+\mathbf{1}_{\{s_i \in bg \}}||s_i-0||^2\]这里的$S_k$是由ground truth确定的语义对象,$s_i$是seed map中的点,函数$1{{s_i \in S_k}}$表示属于前景对象的值为1,属于背景的值为0,反过来,函数$1{{s_i \in bg }}$表示属于背景为1,属于前景对象为0。
$\phi_k(e_i)$为如下公式,计算属于$i$点属于对象$k$的分数。
那为什么要用$s_i$减去$\phi_k(e_i)$,作者认为这个分数应该等于计算由$\phi_k(e_i)$计算出来的值,即这个分数应该等于推理中属于正确语义类别中的分数,而这个属于正确语义类别中的分数由$\phi_k(e_i)$计算出来。
间隙$\sigma$
间隙$\sigma$在实际计算中,是使用的实例在seed map最大分数位置对应到$\sigma \ map$中的$\sigma$值,这里和推理中的$\sigma$是不一致,所以用损失函数(如下)来约束它。
其中,$\sigma_k$是推理中的间隙。
\[\sigma_k = \frac{1}{|S_k|}\sum_{\sigma_i \in S_k} \sigma_i\]基础网络
使用ERFNet,一种编码解码器结构来作为基础网络,将如网络结构图所示,将解码器分开用两次,分别训练不同的参数,实现不同的效果,效果中将网络输出结果叠加到一起,形成了一个4的通道的张量,第一二通道是offset,第三通道是间隙$\sigma$,第四通道是seed map。
xmap与ymap
xmap与ymap由如下代码构造而成。其中2048与1024分别为图像(Cityscas数据集)的宽与高。
xm = torch.linspace(0, 2, 2048).view(1, 1, -1).expand(1, 1024, 2048)
ym = torch.linspace(0, 1, 1024).view(1, -1, 1).expand(1, 1024, 2048)
xym = torch.cat((xm, ym), 0)
损失函数
除了上面对间隙$\sigma$和seed map的分数进行约束的损失之外,还需要优化分割效果的损失,论文中使用二分类损失Lovasz-hinge loss,公式如下,其中又一个雅卡尔指数Jaccard index的概念,其实就是交叠率。
转换为求最小loss
\[\Delta_{J_c(y^*, \bar{y})} = 1 - J_c(y^*, \bar{y})\]求预测像素$i$的hinge loss,其中$F_i(x)$是像素$i$的评分函数的值,而$\bar{y}=sign(F_i(x))$,即$F_i(x)$是没有转为标签之前的分数,$sign(\cdot)$是符号函数,大于$0$,则等于$1$,等于$0$,不变,小于$0$,则等于$-1$,$y_i^*$是像素$i$的标签等于$-1$或者$1$,
再进一步拓展到Lovasz-hinge loss,$\Delta_j^-$是$\Delta_j$的Lovasz拓展。
Lovasz拓展又是什么呢,Lovasz拓展可用于求解次模最小化问题。次模函数的Lovasz拓展是一个凸函数,可高效实现最小化,这里的次模函数看了定义,还是懵的,不纠结这个了,还是继续看Lovasz拓展吧。给定一个次模函数$f$,Lovasz拓展$\hat{f}$如下:
其中,
\[\lambda_i = x_{\pi_{(i)}} - x_{\pi_{(i + 1)}}\]$x_{\pi_{(i)}}$是排好序之后的$x$,
\[1\ge x_{\pi_{(1)}} \ge x_{\pi_{(2)}} \ge ... \ge x_{\pi_{(n)}} \ge 0\]经过相关的推到和证明,得到最后得到Lovasz拓展的次梯度sub-gradients将其作为最小化的对象。
这里只要将$loss_{hinge}{_{\pi(i-1)}}$改成如下公式就可以将二分类Lovasz-hinge loss变成多分类lovasz-softmax loss
参考
损失拓展
论文中提到了对间隔和像素点中心进行拓展。
-
将间隔由圆变成椭圆的间隔,学习二维(x,y)的间隔
\[\phi_k(e_i)=exp\left(-\frac{||e_{ix}-C_{kx}||^2}{2\sigma_{kx}^2}-\frac{||e_{iy}-C_{ky}||^2}{2\sigma_{ky}^2} \right)\] -
将直接取
\[\phi_k(e_i)=exp\left(-\frac{||e_i-\frac{1}{|S_k|}\sum_{e_j\in S_k}e_j||^2}{2\sigma_k^2} \right)\]seed map最大值对应的位置作为中心改为取属于对象的embedding的均值。
很显然的是,第二个拓展,只能用于训练的时候,因为我们需要确定点属于哪个实例,才能通过求均值的方式求中心,论文中为了比较以上的两种拓展,将seed map采样改成了在ground truth上采样,这样直接可以确定点属于哪个实例,从而可以顺利的通过求均值的方式求中心。
训练策略
由于使用Cityscapes数据集,图片比较大h1024xw2048,作者先将图片剪切成500x500,做了100轮预训练,之后在剪切图片1024x1024大小下,进行了50轮的微调,这种方式可以借鉴一下,想起之前还有一种方式,将网络最后的分割层改成改成分类层,在ImageNet数据集上做预训练,只能改回来再在分割的数据集上做分割任务。
论文小结
从这篇论文中学到了什么呢,我觉得主要还是可学习的间隙,然后的话,算是了解一下了做分割的两个损失函数二分类的Lovasz-hinge loss和多分类的lovasz-softmax loss,之后在我们的工作中,我想我会去比较一下交叉熵和lovasz-softmax loss。
看这篇论文,之前卡了我一下的是,之前一直觉得求中心点是个死环,求不出来中心点,在论文中的推理过程中,中心点需要知道哪些点属于实例,而哪些点属于实例需要由有中心点的高斯函数求出来,最后发现作者用逐步取seed map中最大值来确定中心位置和相应位置的间隙,从而可以算哪些点属于实例($\phi_k(e_i) > 0.5$),逐步求实例中心的这个过程其实有点类似于非最大值抑制求极大值的过程,每个极大值代表一个实例的中心。
这篇论文就大概总结到这里了。