这两天在上课之余,看了这篇论文,同学极力推荐,说embedding的效果的非常好(看图一中c图的效果确实很好),而且他跑过了代码,效果确实是不错的,嘿嘿,我来了,总结一下吧,看学到了些什么吧。
效果图
先看效果图吧(图一),图c的embedding效果图确实挺好的。
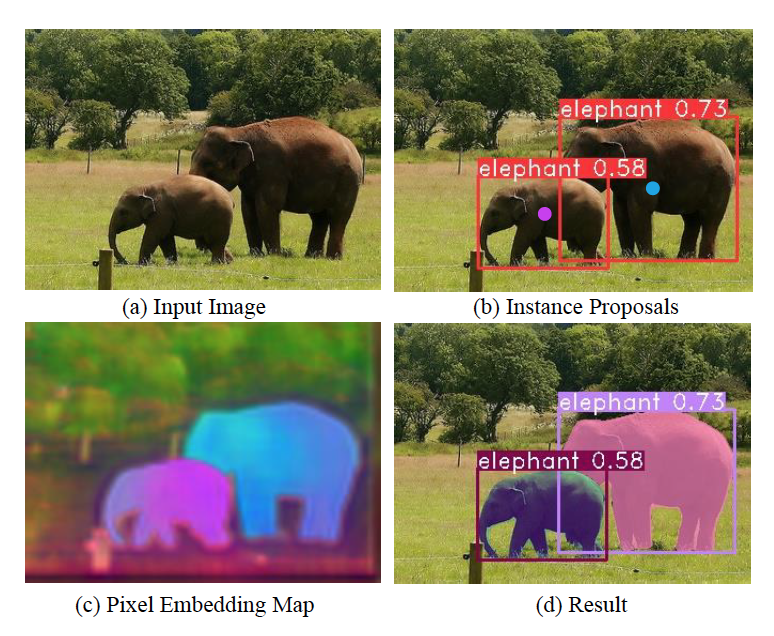
下面来看论文主体内容吧。
摘要与引言
论文一开始就说结合了现在流行的两种实例分割方法:基于分割方法(先分割然后聚类)、基于建议方法(先检测然后预测mask),打到了Mask R-CNN的性能以及速度的同时,文章中的方法是one-stage方法,而Mask R-CNN是具有代表性的two-stage方法。
这里说一下我所理解的one-stage、two-stage以及end-to-end吧。1
论文还提到了Mask R-CNN存在的两个问题:
- “RoIPooling/RoIAlign”(相关概念可以看一下这篇博客)步骤的结果会导致特征的丢失和长宽比变形(the distortion to the aspect ratios),“RoIPooling/RoIAlign”主要的作用是将不同大小的建议框对应的feature map映射到统一大小,方便后续的处理,由于建议框大小不是固定的,所以结果对应到建议框的区域的长宽比可能是变形的(比如建议框大小为大小为665x665,而经过“RoIPooling/RoIAlign”要固定成7*7大小的特征图,这个映射的比例是2.86:1,这个比例不成整数,固而扭曲了长宽比),从而会丢失一些细节。
- 原话:it still sustains weakness in being complex to adjust too many parameters. 我不确定这里的参数是说的模型参数还是超参数,不过我更偏向于是超参数太多。
然后论文中还提到了现在基于分割的one-stage方法,在聚类上有瓶颈,例如有很难确定簇的数量以及簇的中心,从而在性能上不如基于建议方法。
论文中方法结合基于分割方法与基于建议方法,使用两个embedding概念,像素上的嵌入(embedding for pixels),实例建议上的嵌入(embedding for instance proposals,来表示框以及分类),在簇与簇之间使用灵活的间隙(margin)来训练。
EmbedMask
模型
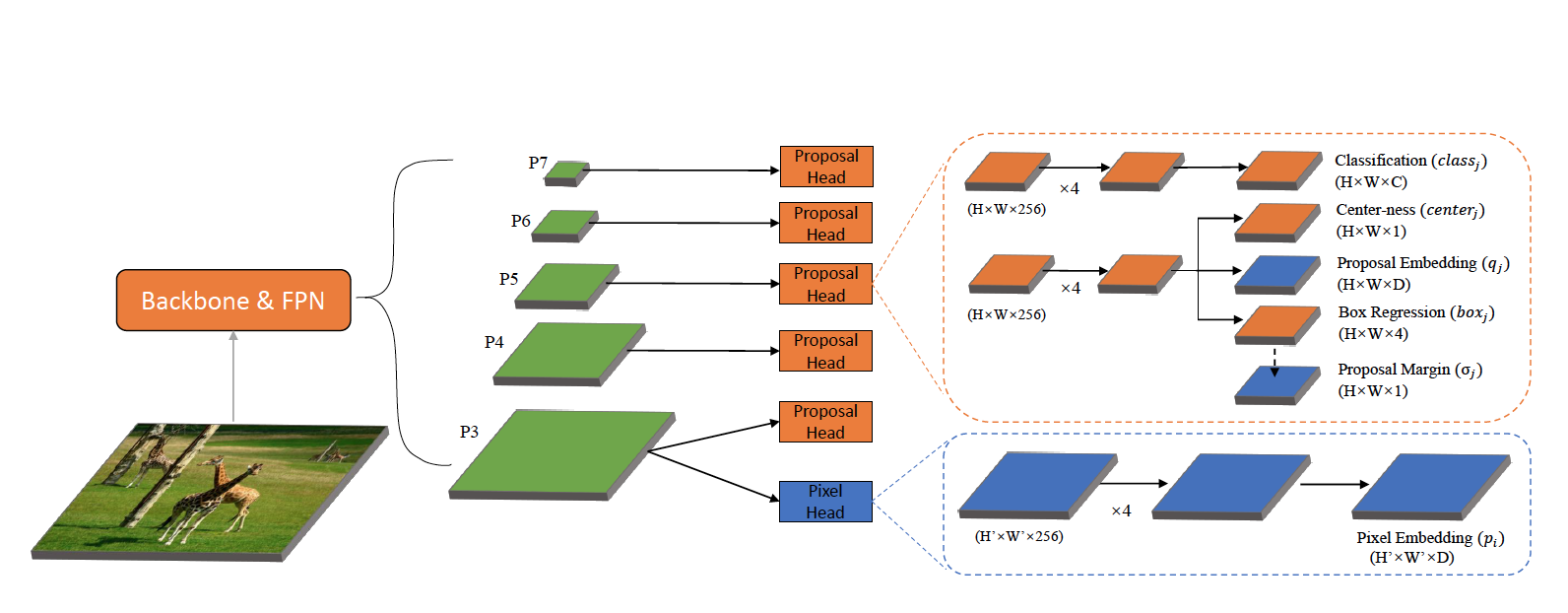
图中模型主体是FCOS模型2(一个物体检测模型),蓝色的部分是论文中新加入的内容,加入了像素级别和建议框上的嵌入以及建议间隙(用来灵活的建议框中像素嵌入向量之间的间隙)。
生成Mask
生成Mask的方法是求像素级别的嵌入向量与建议框的嵌入向量(作为建议框中实例簇的中心)的欧式距离,距离小于margin时,则属于建议框分类的实例,反之不属于,公式如下:
\[Mask_k(x_i) = \begin{cases} 1,\ \ ||p_i-Q_k|| \leq \sigma & \\\\ 0,\ \ ||p_i-Q_k|| > \sigma \end{cases}\]其中$Mask_k(x_i)$是像素点$x_i$属于实例$k$的对应的Mask值,$p_i$是像素点对应的像素级别的嵌入向量,$Q_k$是像素点所属建议框对应分类k的嵌入向量,$\sigma$则是margin。
论文中还提到这个margin是可以学习得到的(由Box Regression经过1x1的卷积后得到,可见模型图),而上面那种常用的方法到这里还并不能学习,而论文中提到参考了一篇论文中的方法,使用高斯函数,将这个margin融入到生成属于分类对象$k$的Mark的概率图中。公式如下:
\[\phi(x_i, S_k) = \phi(p_i, Q_k, \Sigma_k) = exp(-\frac{||p_i-Q_k||^2}{2{\Sigma_k}^2})\]其中$\phi(x_i, S_k)$是指像素点$x_i$属于实例$S_k$的概率,而$\Sigma_k$是实例$k$对应的Margin。(由Box Regression经过1x1的卷积后得到。)
就这样,将Margin融入到了训练参数中,而在训练的时候$Q_k$与$\Sigma_k$与推理的时候的$Q_k$与$\Sigma_k$是有所区别的。训练的时候$Q_k$与$\Sigma_k$的计算公式如下:
\[Q_k = \frac{1}{N_k} \sum_{j\in M_k} q_j\] \[\Sigma_k = \frac{1}{N_k} \sum_{j\in M_k} \sigma_j\]其中$N_k$是在实例$S_k$中正采样的像素点的个数,$M_k$是实例$k$的对应的Mask。
正因为推理的时候与训练的时候的不同,在损失函数上对其进行了约束,见smooth损失。
可学习的的间隙(Margin)
论文中提到了两点使用手动设置固定的margin的问题:
- 找到一个比较好的值相对较难
- 对于多尺度对象的训练不太友好,因为像素级别的嵌入向量在大的对象往往比较发散,而在小的对象却比较集中(即距离的跨度或者说范围与对象大小成正比,当对象越大时,像素嵌入向量的距离的范围跨度会大一些,而对象笔比较小的时候,范围跨度会小一些)。
损失函数
1. 用于优化Mask的损失函数
使用二分类损失函数,公式如下,但在实践中,作者发现使用lovasz-hinge loss3损失更好,这个损失暂时还么了解。
\[L_{mask}=\frac{1}{K}\sum_{k=1}^K\frac{1}{N_k}\sum_{p_i\in B_k}L(\phi(x_i,S_k), G(x_i,S_k))\]其中$L(·)$是二分类(交叉熵)损失、$B_k$ 是实例$k$的对应的推荐框内的像素点集,$\phi(x_i, S_k)$是指像素点$x_i$属于实例$S_k$的概率,$G(x_i,S_k)$是像素点$x_i$属于实例$S_k$的真实值,属于为1,不属于为0。
2. Smooth损失
由于在训练的时候的$Q_k$与$\Sigma_k$与推理的时候的$Q_k$与$\Sigma_k$是有所区别的,所以使用Smooth损失来约束它,让$q_j$与$Q_k$以及$\sigma$与$\Sigma_k$尽量接近。公式如下:
\[\begin{aligned} L_{smooth} & = \frac{1}{K}\sum_{k=1}^K\frac{1}{N_k}\sum_{j\in M_k}||q_j - Q_k||^2 \\ & + \frac{1}{K}\sum_{k=1}^K\frac{1}{N_k}\sum_{j\in M_k}||\sigma_j - \Sigma_k||^2 \end{aligned}\]其中$M_k$是实例$k$的对应的Mask。
3. 整体的损失
整体的损失公式如下:
\[L=L_{cls}+L_{center}+L_{box}+\lambda_1L_{mask}+\lambda_2L_{smooth}\]其中原始分类的损失$L_{cls}$、中心损失(center-ness loss)$L_{center}$、边框回归损失(box regression loss)$L_{box}$还是沿用FCOS那篇论文中的,而加了上面提到的两个损失$L_{mask}$、$L_{smooth}$。
模型整个处理过程
EmbedMask整个过程大概是:给定一张图片,通过修改后的物体检测网络FCOS,经过NMS(non-maximum suppression,非极大值抑制),得到最终建议的实例集$S$,对应这个实例集中的实例$S_k$有它的边框值、类别分数、推荐边框的嵌入向量$q_j$、推荐边框的间隙(Margin)$\sigma_j$,计算代表实例k的嵌入向量$Q_k$和可学习的阈值$\Sigma_k$,再通过计算$\phi(x_i, S_k)$($\phi(p_i, Q_k, \Sigma_k)$)得到$x_i$属于$S_k$的概率,设置阈值为0.5,生成最终Mask。
总结与感受
首先这个网络主体是使用的物体检测网络FCOS,加入了像素上的嵌入,实例建议上的嵌入,对这些我的感触都不大,最让我感觉学到了的是可学习的间隙(margin),我们当前的课题,是使用的固定的间隙,也确实遇到多尺度对象的训练效果不好的问题,我想之后我们得使用类似论文中的方法改进这点,算是意外收获了,还有就是结合使用中间层的特征,我们暂时还没有用起来,一直有提说要用上,看这篇论文也是这样用的。
好了,先记录到这了。