带有歧视的损失函数的语义实体分割(Semantic Instance Segmentation with a Discriminative Loss Function)
论文提出一种将特征空间的点分簇的损失函数,损失函数主要分为三项构成,分别为方差项(variance term),距离项(distance term),正则项(regulariztion trem),其中方差项计算的是簇内的距离,距离项计算的是簇与簇的距离,分别控制同簇点与簇中心之间的距离在δv之内,不同簇与簇的中心距离大于δd,论文下载地址
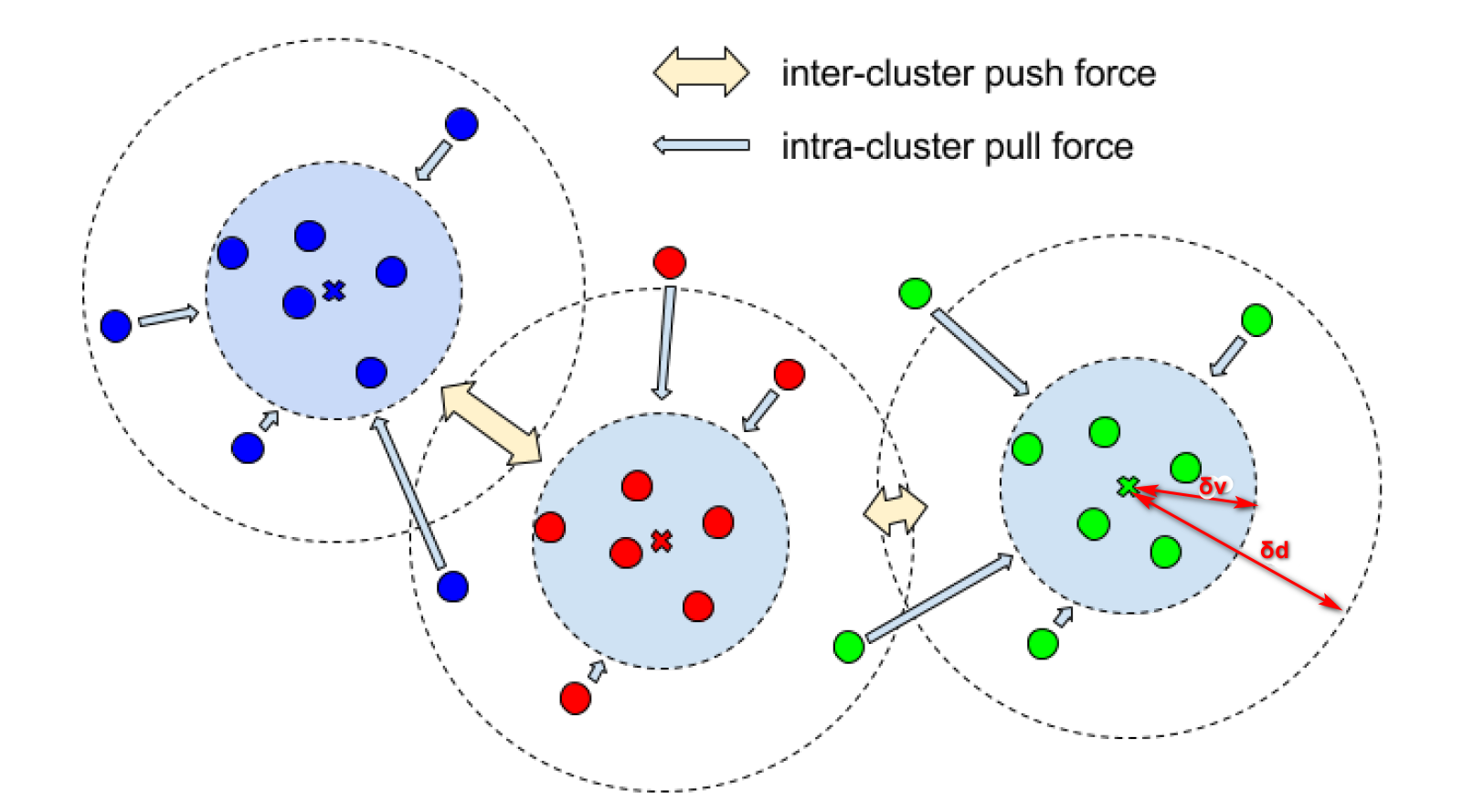
论文主要关注于损失函数,主要关注于训练出好的特征空间(如Embedding Space)。
带有歧视的损失函数
定义
$C$是真实值中的簇的总数,$N_c$簇$c$中的元素数量,$x_i$是一个元素对应的嵌入向量,$\mu_c$是&c&簇中嵌入向量的平均值(簇的中心),$\vert\vert\cdot\vert\vert$是L1距离或者L2距离,$[x]_+$是max(0,x)定义的铰链函数,$\delta_v$和$\delta_d$代表方差和距离损失的间隙。
方差项
\[L_{var} = \frac{1}{C}\sum_{c=1}^C\frac{1}{N_c}\sum_{i=1}^{N_c}[||{\mu_i-x_i}||-\delta_v]_+^2\]距离项
\[L_{dist}=\frac{1}{C(C-1)}{\sum_{c_A=1}^{C}\sum_{c_B=1}^{C}}_{c_A \neq c_B}[2\delta_d-||{\mu_{c_A}-\mu_{c_B}}||]_+^2\]正则项
\[L_{reg}=\frac{1}{C}\sum_{c=1}^{C}||\mu_c||\]完整损失函数
\(L=\alpha\cdot{L_{var}}+\beta\cdot{L_{dist}}+\gamma\cdot{L_{reg}}\)
在实验时,作者设置$\alpha=\beta=1$,$\gamma=0.001$。
其他内容
论文还说到了后处理(post-processing),包括增强鲁棒性(increasing robustness)等等, 还有其他实验的设置和数据集,还有优缺点等等,这里最后说一下这个方法的优缺点(pros and cons)。
优缺点
论文中方法,在有重叠部分的情况下依然有好的效果,比如在合成的零散的线条中,在数据集图片中有比较相似的实例时,效果也比较好,但是,在随机多种多样的数据集中,效果不太好,在只有一个的实例对象的图片中训练效果不是太好。